See on geomeetriline keha, mis on piiratud kahe paralleelse tasandi ja silindrilise pinnaga.

Silinder koosneb külgpinnast ja kahest alusest. Silindri pindala valem sisaldab eraldi aluste ja külgpinna pindala arvutamist. Kuna silindri alused on võrdsed, arvutatakse selle kogupind järgmise valemi abil:

Vaatleme silindri pindala arvutamise näidet pärast kõigi vajalike valemite tundmist. Kõigepealt vajame silindri aluse pindala valemit. Kuna silindri põhi on ring, peame rakendama:
Peame meeles, et nendes arvutustes kasutatakse konstantset arvu Π = 3,1415926, mis arvutatakse ringi ümbermõõdu ja selle läbimõõdu suhtena. See arv on matemaatiline konstant. Vaatame veidi hiljem ka näidet silindri aluse pindala arvutamisest.

Silindri külje pindala

Silindri külgpinna pindala valem on aluse pikkuse ja kõrguse korrutis:

Nüüd kaaluge probleemi, mille puhul peame arvutama kogupindala silinder. Antud joonisel on kõrgus h = 4 cm, r = 2 cm. Leiame silindri kogupindala.
Esiteks arvutame aluste pindala:
Nüüd kaaluge silindri külgpinna arvutamise näidet. Laiendatuna on see ristkülik. Selle pindala arvutatakse ülaltoodud valemi abil. Asendage kõik andmed sellesse:
Ringi kogupindala on kahekordse aluse ja külje pindala summa:

Seega, kasutades joonise aluste pindala ja külgpinna valemeid, saime leida silindri kogupindala.
Silindri telglõik on ristkülik, mille küljed on võrdsed silindri kõrguse ja läbimõõduga.

Silindri aksiaallõike pindala valem tuletatakse arvutusvalemist:

Leidke silindri põhjaga risti oleva aksiaalse sektsiooni pindala. Selle ristküliku üks külg on võrdne silindri kõrgusega, teine on võrdne põhiringi läbimõõduga. Sellest lähtuvalt on ristlõike pindala sel juhul võrdne ristküliku külgede korrutisega. S=2R*h, kus S on ristlõike pindala, R on põhiringi raadius, mis on antud ülesande tingimustega, ja h on silindri kõrgus, mis on samuti antud ülesande tingimustega.

Kui lõik on alustega risti, kuid ei läbi pöörlemistelge, ei võrdu ristkülik ringi läbimõõduga. See tuleb välja arvutada. Selleks tuleb ülesandes öelda, millisel kaugusel pöördeteljest lõiketasand läbib. Arvutuste hõlbustamiseks konstrueerige silindri põhjast ring, tõmmake raadius ja eraldage sellele kaugus, mille kaugusel sektsioon asub ringi keskpunktist. Sellest punktist tõmmake perpendikulaaridesse, kuni need ristuvad ringiga. Ühendage ristumispunktid keskpunktiga. Peate leidma akordid. Leia poole akordi suurus Pythagorase teoreemi abil. See võrdub ruutjuur ringi raadiuse ruutude erinevusest tsentrist lõikejooneni. a2=R2-b2. Kogu akord on vastavalt võrdne 2a. Arvutage ristlõike pindala, mis võrdub ristküliku külgede korrutisega, st S=2a*h.

Silindri saab lahti lõigata ilma aluse tasapinda läbimata. Kui ristlõige on pöörlemisteljega risti, on see ring. Selle pindala on sel juhul võrdne aluste pindalaga, see tähendab, et see arvutatakse valemiga S \u003d πR2.

Kasulikud nõuanded

Sektsiooni täpsemaks ettekujutamiseks tehke sellele joonis ja lisakonstruktsioonid.

Allikad:

silindri ristlõike pindala

Pinna ja tasapinna lõikumisjoon kuulub nii pinna kui ka lõiketasandi alla. Silindrilise pinna ja sirge generatriksiga paralleelse lõiketasandi lõikejoon on sirgjoon. Kui lõiketasand on pöördepinna teljega risti, on sektsioonil ring. Üldjuhul on silindrilise pinna ja lõiketasandi lõikejoon kõverjoon.

Sa vajad

Pliiats, joonlaud, kolmnurk, mustrid, kompassid, mõõteriist.

Juhend

Frontaalprojektsioonitasandil P2 kattub lõikejoon sirgjoone kujul oleva lõiketasandi Σ₂ projektsiooniga.
Määrake silindri generatriksi lõikepunktid projektsiooniga Σ₂ 1₂, 2₂ jne. punktidele 10₂ ja 11₂.

Tasapinnal P₁ on ring. Lõiketasandil Σ₂ märgitud punktid 1₂ , 2₂ jne. projektsioonijoone abil projitseeritakse ühendused selle ringi kontuurile. Määrake nende horisontaalsed projektsioonid sümmeetriliselt ringi horisontaaltelje suhtes.

Seega määratletakse soovitud lõigu projektsioonid: tasapinnal P2 - sirgjoon (punktid 12, 2₂ ... 102); tasapinnal P₁ - ring (punktid 1₁, 2₁ ... 10₁).

Kahe võrra konstrueerida etteantud silindri lõigu loomulik suurus eesmise projektsioonitasandi Σ järgi. Selleks kasutage projektsioonide meetodit.

Joonistage tasapind P4 paralleelselt tasandi Σ₂ projektsiooniga. Märkige sellele uuele x₂4 teljele punkt 1₀. Kaugused punktide 1₂ - 2₂, 2₂ - 4₂ jne vahel. tõmmake lõigu esiprojektsioonist x24-teljele kõrvale, tõmmake projektsiooniühendusele õhukesed jooned risti x24-teljega.

AT seda meetodit tasand P4 asendatakse tasapinnaga P1, seetõttu kandke horisontaalprojektsioonist mõõtmed teljelt punktidesse P4 tasandi teljele.

Näiteks punktide 2 ja 3 puhul P₁ on see kaugus punktidest 2₁ ja 3₁ teljeni (punkt A) jne.

Kui olete horisontaalprojektsioonist näidatud kaugused edasi lükanud, saate punktid 2₀, 3₀, 6₀, 7₀, 10₀, 11₀. Seejärel määratakse ehituse suurema täpsuse huvides kindlaks ülejäänud, vahepealsed punktid.

Ühendades kõik punktid kõvera kõveraga, saate silindri ristlõike soovitud loomuliku suuruse eesmise eenduva tasapinna järgi.

Allikad:

kuidas lennukit vahetada

Vihje 3: kuidas leida kärbitud koonuse teljesuunalise osa pindala

Lahendada see ülesanne, on vaja meeles pidada, mis on kärbitud koonus ja millised omadused sellel on. Kindlasti joonistage. See määrab, milline geomeetriline kujund on sektsioon. On täiesti võimalik, et pärast seda ei ole probleemi lahendamine teile enam keeruline.

Juhend

Ümmargune koonus on keha, mis saadakse kolmnurga pööramisel ümber selle ühe jala. Ülevalt tulevad sirged jooned koonused ja selle baasi ristuvat nimetatakse generaatoriteks. Kui kõik generaatorid on võrdsed, on koonus sirge. Ringi põhjas koonused asub ring. Ülevalt alusele langetatud risti on kõrgus koonused. Ümmarguse sirge juures koonused kõrgus langeb kokku selle teljega. Telg on sirgjoon, mis ühendab aluse keskpunkti. Kui horisontaalne lõiketasapind ringikujuline koonused, siis selle ülemine alus on ring.

Kuna probleemi seisukorras pole seda täpsustatud, siis on see koonus see, mis on sisse antud sel juhul, võime järeldada, et see on sirge kärbitud koonus, mille horisontaalne osa on alusega paralleelne. Selle telglõik, s.o. vertikaaltasand, mis läbi ringikujulise telje koonused, on võrdhaarne trapets. Kõik aksiaalsed lõigudümmargune sirge koonused on üksteisega võrdsed. Seetõttu, et leida ruut aksiaalne lõigud, on vaja leida ruut trapets, mille alusteks on kärbitud aluste läbimõõdud koonused, ja küljed on selle generaatorid. Kärbitud kõrgus koonused on ka trapetsi kõrgus.

Trapetsi pindala määratakse valemiga: S = ½(a+b) h, kus S on ruut trapets; a - trapetsi alumise aluse väärtus; b - selle ülemise aluse väärtus; h - trapetsi kõrgus.

Kuna tingimus ei täpsusta, millised on antud, siis on võimalik, et kärbitud mõlema aluse diameetrid koonused teada: AD = d1 on kärbi alumise aluse läbimõõt koonused;BC = d2 on selle ülemise aluse läbimõõt; EH = h1 - kõrgus koonused.Sellel viisil, ruut aksiaalne lõigud kärbitud koonused defineeritud: S1 = ½ (d1+d2) h1

Allikad:

kärbitud koonuse piirkond

Silinder on kolmemõõtmeline kujund ja koosneb kahest võrdsest alusest, mis on ringid, ja külgpinnast, mis ühendab aluseid piiravaid jooni. Arvutada ruut silinder, otsige üles kõigi selle pindade pindalad ja liitke need kokku.

Silinder on geomeetriline keha, mis on piiratud kahe paralleelse tasandi ja silindrilise pinnaga. Artiklis räägime sellest, kuidas leida silindri pindala ja valemi abil lahendame näiteks mitmeid probleeme.

Silindril on kolm pinda: ülemine, alumine ja külgpind.

Silindri ülemine ja alumine osa on ringikujulised ja neid on lihtne määratleda.

On teada, et ringi pindala on võrdne πr 2 . Seetõttu näeb kahe ringi (silindri üla- ja alaosa) pindala valem välja selline: πr 2 + πr 2 = 2πr 2 .

Kolmas, silindri külgpind, on silindri kumer sein. Selle pinna paremaks kujutamiseks proovime seda transformeerida, et saada äratuntav kuju. Kujutage ette, et silinder on tavaline plekkpurk, millel pole ülemist kaant ja põhja. Teeme külgseinale vertikaalse sisselõike purgi ülaosast allapoole (joonisel 1. samm) ja proovime saadud kujundit võimalikult palju avada (sirgendada) (2. samm).

Pärast saadud purgi täielikku avalikustamist näeme tuttavat joonist (3. samm), see on ristkülik. Ristküliku pindala on lihtne arvutada. Aga enne seda pöördume korraks tagasi algse silindri juurde. Algsilindri tipuks on ring ja me teame, et ringi ümbermõõt arvutatakse valemiga: L = 2πr. See on joonisel märgitud punasega.

Millal külgsein silinder on täielikult laienenud, näeme, et ümbermõõt muutub saadud ristküliku pikkuseks. Selle ristküliku külgedeks on silindri ümbermõõt (L = 2πr) ja kõrgus (h). Ristküliku pindala on võrdne selle külgede korrutisega - S = pikkus x laius = L x h = 2πr x h = 2πrh. Selle tulemusena oleme saanud valemi silindri külgpinna arvutamiseks.

Silindri külgpinna pindala valem
S pool = 2prh

Silindri täispind

Lõpuks, kui liidame kokku kõigi pindala kolm pinda, saame silindri kogupindala valemi. Silindri pindala on võrdne silindri ülaosa pindalaga + silindri põhja pindalaga + silindri külgpinna pindalaga või S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Mõnikord kirjutatakse see avaldis identse valemiga 2πr (r + h).

Silindri kogupindala valem
S = 2πr 2 + 2πrh = 2πr(r + h)
r on silindri raadius, h on silindri kõrgus

Näited silindri pindala arvutamiseks

Ülaltoodud valemite mõistmiseks proovime näidete abil arvutada silindri pindala.

1. Silindri aluse raadius on 2, kõrgus on 3. Määrake silindri külgpinna pindala.

Kogupindala arvutatakse valemiga: S pool. = 2prh

S pool = 2 * 3,14 * 2 * 3

S pool = 6,28 * 6

S pool = 37,68

Silindri külgpindala on 37,68.

2. Kuidas leida silindri pindala, kui kõrgus on 4 ja raadius on 6?

Kogupindala arvutatakse valemiga: S = 2πr 2 + 2πrh

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Silindri raadiuse valem:
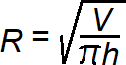
kus V on silindri maht, h on kõrgus

Silinder on geomeetriline keha, mis saadakse ristküliku pööramisel ümber selle külje. Samuti on silinder keha, mida piirab silindriline pind ja kaks paralleelset tasapinda, mis seda lõikuvad. See pind tekib siis, kui sirgjoon liigub endaga paralleelselt. Sel juhul liigub valitud sirge punkt mööda teatud tasast kõverat (juhikut). Seda sirget nimetatakse silindrilise pinna generatriksiks.
Silindri raadiuse valem:
kus Sb - külgpindala, h - kõrgus

Silindri iga aluse pindala on π r 2, on mõlema aluse pindala 2π r 2 (joonis).

Silindri külgpinna pindala on võrdne ristküliku pindalaga, mille alus on 2π r, ja kõrgus on võrdne silindri kõrgusega h, st 2π rh.

Silindri kogupind on: 2π r 2+2π rh= 2π r(r+ h).

Võetakse silindri külgpinna pindala pühkimisala selle külgpind.

Seetõttu on parempoolse ringikujulise silindri külgpinna pindala võrdne vastava ristküliku pindalaga (joonis) ja arvutatakse valemiga

S b.c. = 2πRH, (1)

Kui lisame silindri kahe aluse pindala silindri külgpinna pindalale, saame silindri kogupindala

S täis \u003d 2πRH + 2πR 2 \u003d 2πR (H + R).

Sirge silindri maht

Teoreem. Parempoolse silindri maht võrdub selle aluse pindala ja kõrguse korrutisega , st.

kus Q on aluspind ja H on silindri kõrgus.

Kuna silindri põhipindala on Q, on piiritletud ja sisse kirjutatud hulknurkade jadad pindalaga Q n ja Q' n selline, et

\(\lim_(n \paremnool \infty)\) K n= \(\lim_(n \paremnool \infty)\) Q' n= Q.

Koostame prismade jadad, mille alusteks on ülalpool vaadeldud kirjeldatud ja sisse kirjutatud hulknurgad ning mille külgservad on paralleelsed antud silindri generaatoriga ja pikkusega H. Need prismad on kirjeldatud ja sisse kirjutatud antud silindri jaoks. Nende mahud leitakse valemite abil

V n= Q n H ja V' n= Q' n H.

Järelikult

V= \(\lim_(n \paremnool \infty)\) Q n H = \(\lim_(n \paremnool \infty)\) Q' n H = QH.

Tagajärg.
Parempoolse ringikujulise silindri maht arvutatakse valemiga

V = π R 2 H

kus R on aluse raadius ja H on silindri kõrgus.

Kuna ringikujulise silindri alus on ring raadiusega R, siis Q \u003d π R 2 ja seetõttu